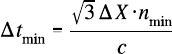
A. TEMPEST and General FDTD Information
POEMS relies on the finite-difference time domain algorithm of Yee for its calculations. The
Yee algorithm simulates the Maxwell curl equations directly, on two interpenetrating grids,
half a step apart in each axis: one for H and one for E. Because each E component is
completely surrounded by H nodes, and vice-versa, Ampere’s and Faraday’s laws can be
simulated in small-scale integral form, rather than differential form, and because the desired
simulation point is exactly in the middle of the block, the Yee algorithm achieves second-
order accuracy in both space and time.
Compared with finite-element techniques, FDTD tends to be faster but much more memory-
intensive, because each cell requires six floats for the field components plus (in the simplest
implementation) an int specifying which of the known materials occupies the cell. FDTD is
also harder to apply on an irregular grid, so most FDTD codes specify a uniform cubical grid
over the whole simulation domain, and FIDO/TEMPEST is no exception. There’s a very great
deal of information about FDTD and related methods in Taflove & Hagness, Computational
Electrodynamics: the Finite Difference Time Domain Method., 2nd Ed., Artech, 2000.
1. Startup and Steady State
TEMPEST uses a hard-coded 2-cycle soft start. By turning on the sources gradually, settling
artifacts are reduced and convergence time reduced. For many purposes, e.g. computing
amplitudes, phases, Poynting vectors, and power dissipation density, both the real and
imaginary parts of the field variables are required. POEMS computes these by the simple
expedient of letting FIDO/TEMPEST run for an extra quarter cycle, which works fine for steady
state, but gives rise to edge artifacts in transient simulations. These artifacts, which can be
seen clearly in Figure 2.9, arise because the quadrature component has had a quarter cycle
longer to propagate into the simulation domain, so its leading edge and the two-cycle taper
are in different places compared with those of the in-phase component, giving rise to odd
ripples and unphysical apparent energy sources and sinks.
2. Time step
Being a nearest-neighbour algorithm, FDTD advances information across the grid at the rate
of one block per time step. As one might expect, if this rate is faster than the speed of light
in the materials, the simulation becomes unstable. Because of the interpenetrating grids for E
and H, the simulation actually proceeds in half-steps, deriving H from E and then E from H.
Adjacent E and H nodes are separated by half the body diagonal of a cell, and the minimum
half-step is the time taken to cross this distance in the fastest (lowest-index) material. Thus
the minimum full time step ∆t
min
is given by
TEMPEST chooses its time step just longer than this value, and then adds a little more to make
sure that the number of time steps per period (period_step) is an integer divisible by 4.
This isn’t numerology. We usually need to get in-phase (I) and quadrature (Q) field
components for further processing. The I and Q components are a quarter cycle apart, so
choosing the time step this way avoids the need for interpolation.
49


















