3.2. The Computational Domain
3.2.1. Symmetry
Many technologically useful devices have a periodic structure. The periodic boundary
conditions assumed by POEMS are a natural fit to such structures, which can be simulated
very efficiently. This happens automatically if you leave out the absorbers on the sides
facing the periodic direction. Almost as many devices exhibit symmetry planes. A
domain with a symmetry plane, illuminated symmetrically, will exhibit completely
symmetric fields, so no extra information is generated by simulating both halves.
Splitting the domain in half down the symmetry boundary can save half the run time and
half the memory, while preserving the same level of detail in the results. Domains with
more than one symmetry boundary save even more (though this begins to restrict the
illumination more severely). POEMS (via support built into TEMPEST, FIDO, and EMPOST)
supports symmetrical simulations.
0
1
2
3
4
1
2
3
4
0 1 2 3 4 5 6 7 8
Image Domain
Actual Domain
Next Period
N rows
N-2 Rows
Unfolded
2N-2 Rows
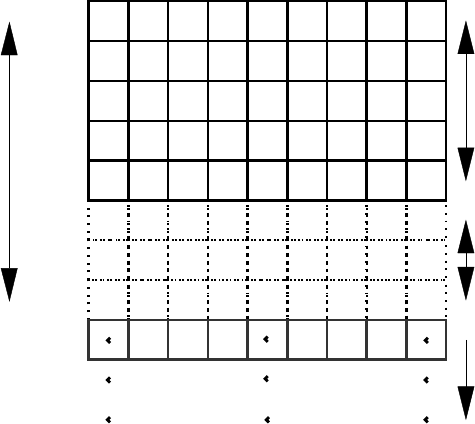
Figure 2.2 Geometry of a symmetry boundary with N=5
It’s important to visualize the symmetry arrangement correctly, and it isn’t what one
might first think: A symmetry plane actually slices right through the centre of the
outermost elements. Say the X axis has 100 cells, numbered 0-99. Normally, periodic
boundary conditions apply, and cell 0’s neighbours are 1 and 99. If X is a symmetry
direction, cell 0’s neighbour is cell 1 on both sides. That is, a 1-block wide layer lying
against the symmetry axis has the same effect as a 1-block layer in the middle of the
unfolded domain. A 2-block layer against the symmetry axis is equivalent to a 3-block
layer down the middle of the unfolded domain.
31


















